This is a follow-up article to last week's piece. It gives a lot more information on the subject and provides the basis for this experiment, so I highly recommend looking there first.

A few weeks ago, I did an experiment that tested out the Wisdom Of The Crowd. As I mentioned in the previous article, I'd been interested in the topic for a long time, And eventually I decided to perform the experiment myself. In short, I filled an empty cookie jar with popcorn, and told people around me to guess how many kernels of popcorn were in the jar. After recording all of the guesses, I analyzed the data to see how accurate it was. My hypothesis was that the average of all the guesses would be more accurate than any of the guesses themselves.

(A picture of me while I am tallying the guesses)

The last article was mainly focused the experiment itself and how it played out. But now that I've analyzed my data, I'll present my findings to you in this article.

The Results

The results of my experiment were different from what I expected, in both good and bad ways.

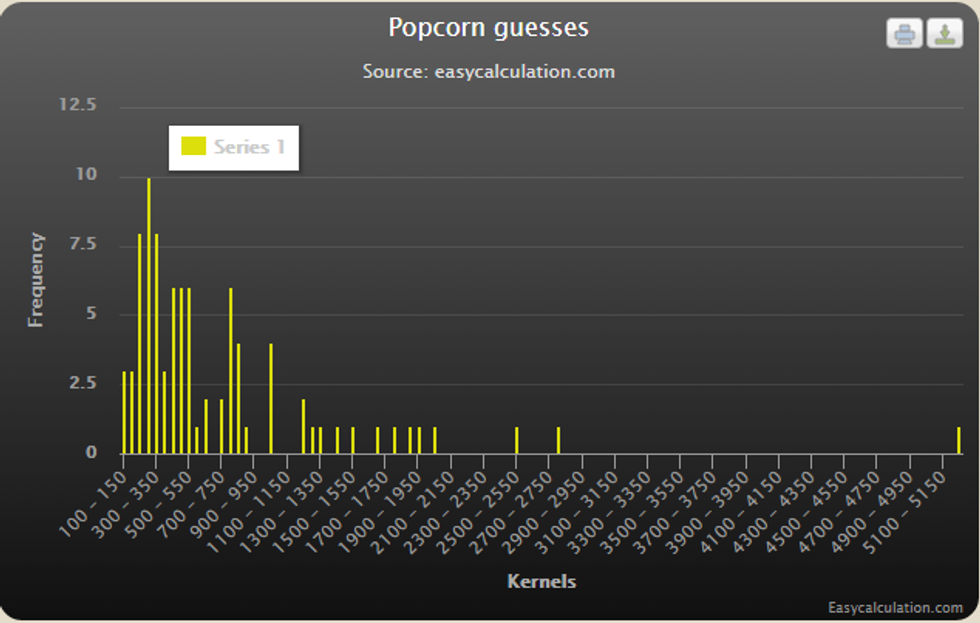
First of all, there is the straightforward analysis of the experiment, where I took all of the guesses and found the average of them. In total, there were 87 guesses that I collected. They ranged from a low of 100 kernels to a high of 5210 kernels, with most guesses falling at around 300 kernels. There were 2 groups of people that I surveyed, one group from the first day of surveying and the other from the second day; this will be important later on. The sum of all the guesses was 60765, leading to an average guess of 698.45 kernels when rounded to the nearest 100th of a kernel.

(a histogram of all the answers I received)

So what happened? That's a disappointing 19.2244% difference from the actual guess, which is high when compared to the less than 1% difference that I would've expected due to other similar experiments. I really had a lot of faith in this concept, so I refrained from giving up and I dug further in.

To corroborate this finding, I took the median of the data set as well. That turned out to be 465, a devastating 58.2317% difference from the actual number of kernels. That disappointed me, but I pressed on, and this is where the different sections come in. The first section had 50 guesses and fetched an average guess of 591.78--a 35.47% difference from the actual guess. But the second set, which had 37, had an average of 842.594--a more desireable 0.5215% difference.

To make sure that this wasn't just a coincidence, I took a random set of 37 values from the first set, and then another random 37 from all of the data combined. They had an average of 640.513 for the former, and 675.513 for the former; that's a difference of 27.76% and 22.52%, respectively.

I have a theory as to why this is so. On the first day, I asked more people, and was a bit more lenient about my rule on frivolous guesses. On the second day, I took my time more, and was able to ask more informed people, such as staff and teachers. Additionally, that was the day that I had all of my core classes, like English and Math, which for various reasons might have more knowledgeable people. These things tie in to the fact that Surowiecki wrote about in his book, that the group of people being sampled must have a good amount of intelligence in order to maintain intelligence for the group as a whole.

Conclusion

In my opinion, this experiment was a mild success. It still proved the concept well enough, but I needed to do some more digging before I could find what I was looking for. Regardless, I had a good learning experience, and in the future I might perform this same experiment again but with stricter guidelines and a larger sample size.