This weekend, my boyfriend and I went to see 1-2-3-Φ: Math and Art, “a group exhibit about the inspiration of mathematical concepts in art” at Studio Place Arts in Barre, Vermont. Though the map between art and math may not be a simple linear transformation, the fields connect in a variety of ways. While the definition of art is complex and necessarily vague, for the sake of simplicity, this article is going to focus on traditional visual medium art such as prints, paintings, and sculptures.

Mathematical principles have always played a prime importance in creating art. Symmetry, angles and curves show simple math concepts important to art. The idea of linear perspective allowed for depth and increased realism that revolutionized European painting between the Middle Ages and the Renaissance. More unique math, such as the Golden Ratio, have been seen in many classic works, such as the Mona Lisa.

The Golden Ratio is an irrational number defined by if a line is divided into segments a and b, the ratio of (a+b)/a is equal to the ratio of a/b. Though it is unclear whether it has always been intentionally used by artists, the Golden Ratio has been seen in the works of artists from Da Vinci to Salvador Dali.

Beyond being just a tool used by artists, math can be a source of inspiration and art itself. From the Math and Art exhibit at Studio Place Arts, the work “Duals” by Robert Fathauer shows the relationship between cubes and octahedrons. Cubes and octahedrons form a polyhedron pair in geometry known as a dual, where the vertices of one shape correspond to the center of each face of the other.

The representation of this elegant geometric relationship creates a modern art piece that emphasizes the initial values of minimalism in broadening the definition of art.

Continuing with geometry, it would be irrational to talk about math art and not discuss fractals. Fractals are complex patterns that are self-similar across many scales, creating what is essentially a never ending design. Fractal patterns are extremely common in nature, from the branching of trees to the divergence of rivers into tributaries. In looking at fractals, math can replicate the art we see in our world, while also creating fantastic abstract art, such as prints of the Mandelbrot set.

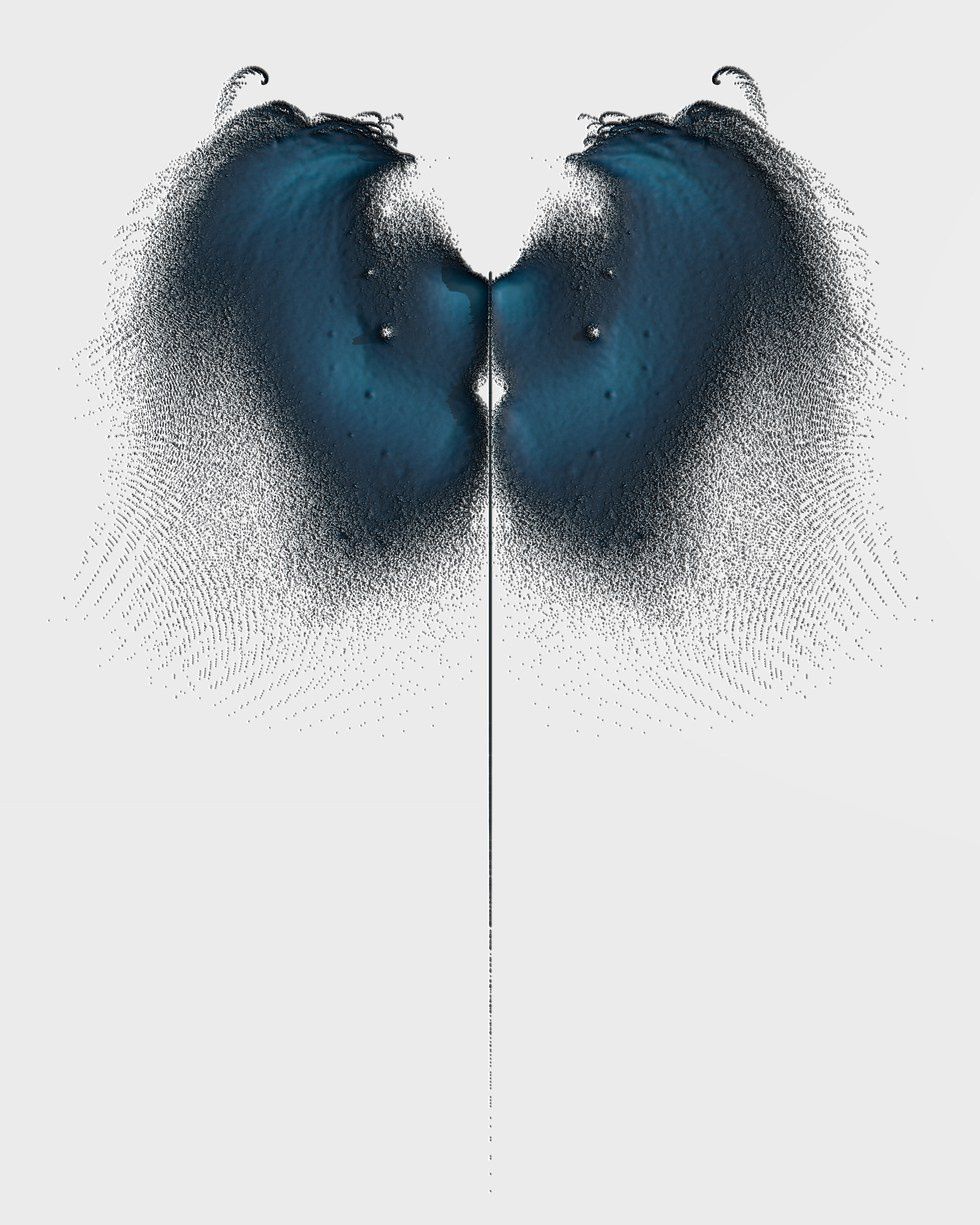
The fractal of the Mandelbrot set is generated from visualizing the solution to specific function. Visualizations of mathematical solutions can create stunning pieces of art, such as “Manifold” by University of Vermont math professor Greg Warrington.

On his webpage, Professor Warrington provides the description

The Kazhdan-Lusztig polynomials are a particularly rich family of polynomials arising from representation theory and the geometry of the flag manifold that I am attempting to understand combinatorially. This image depicts the reciprocals of the roots of the 726,636 distinct Kazhdan-Lusztig polynomials associated to the exceptional Coxeter group H_4. The positive x-axis is pointing directly up. Shading is derived from the density of roots.

While difficult to understand, the image rendered from associating colors to associated solutions is beautiful. The math behind the print’s creation only adds depth to the visual. Solely as a piece of art, in my un-scholarly opinion, “Manifold” has a haunting naturalism to it, evoking thoughts of both the ocean and flight, while moody colors and vaguely fingerprint-like fringes add to the sense of opacity. Understanding the math behind the image adds a sense of intellectualism and reason. Playing against the initial visual response of the art, the cognitive understanding works to create a richer experience of the work.

Math and art often seem like two completely opposing things. But when looking at the universe, they are constantly intertwining. Though not always necessary in finding joy in each of the subjects, having an understanding and appreciation for both can create a much fuller beauty.