In our elementary school math classes, we were often presented sequences of numbers and tasked to find the next term.

1, 2, 3, 4, _____

3, 6, 9, 12, _____

1/2, 1/4, 1/8, 1/16 _____

The answers are 5, 15, and 1/32—simple enough. However, as we soon discovered, math likes to become more complicated over time. We go from addition to multiplication to exponents to derivatives and onward. The next step past a sequence is a series. A series is a sum of the elements in a sequence. They can be finite (only some numbers are added from the sequence), or they can be infinite (every number is added together).

If we added 1, 2, 3, 4, and 5, we get 15. The sequence 1, 2, 3, 4… is known as the natural number sequence, and there is a special formula for quickly adding this series.

Sum=n*(n+1)*(1/2)

The variable n represents the number of numbers from the sequence we want to add. For example, if we wanted to add the first 5 numbers of the sequence, we plug in 5 for n. When we do that, it gives us 15 confirming our result from above.

What if we wanted to add every single natural number together? There is an infinite amount of natural numbers, but we can’t plug in infinity into a formula. Since we are adding an infinite number of positive numbers, we can reasonably say that the sum is infinite.

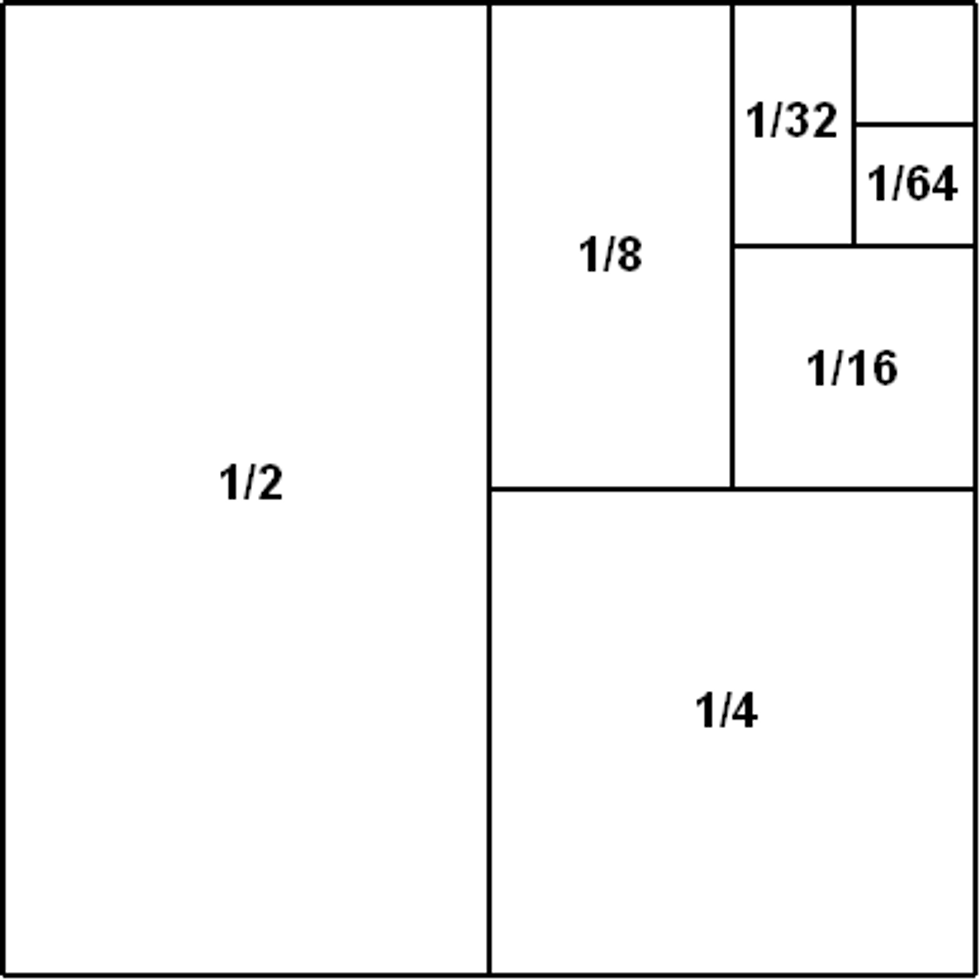
Is there a series whose sum provides a finite number? The series 1/2+1/4+1/8… actually adds to positive 1. The proof for this is somewhat complicated, but it is easily visualized in the following picture.

We can see that every number is the series perfectly fits into a 1x1 square. If we add every sections value (thereby summing the whole series), we get the area of the square. The area of a 1x1 square is 1.

Math likes to be confusing, and some times it proves counterintuitive. Is there a way to warp the natural number series to produce a finite answer? A famous mathematician known as Ramanujan argued that the sum of every natural number equals -1/12.

There are several reasons to claim this ridiculous result, but the following is the simplest. Before we tackle the sum of the natural series, let’s look at another series.

T=1-2+3-4+5-6…

This looks like the natural number series except the sign reverses every term. T is a variable denoting the sum of this series. Let’s multiple both sides by 4.

4T= (1-2+3-4+5-6…)+(1-2+3-4+5-6…)+(1-2+3-4+5-6…)+(1-2+3-4+5-6…)

Rather than multiply each term by 4, I added the series 4 times so I can rearrange some terms to cancel them out. The easiest way to do this is to stack these 4 series vertically. The bottom most row represents the sum.

4T=

We can see that shifting the 2^nd and 3^rd series by one place and shifting the 4^th series by two places, we obtain the following result.

4T=1

T=1/4

What does this have to do with the original natural number series? Let’s denote the sum of the natural number series as S. 4S is the natural number series multiplied by 4.

S= 1+2+3+4+…

4S= 4+8+12+…

If we calculate S-4S, we get

S-4S =-3S = (1+2+3+4…) – (4+8+12+…)

If we distribute the minus sign and rearrange the terms, we get

-3S = 1+(2-4)+3+(4-8)+…

-3S = 1-2+3-4…

We calculated the value of 1-2+3-4… to be 1/4 above, so we can plug that in and divide both sides by -3 to obtain

-3S=1/4

S=-1/12

Is this actually real, or have I pulled some trick? The answer is both, and the "trick" lies in the meaning of the word “sum.” The traditional sum of the natural number series is indeed infinity. It has been proven that manipulating the order of a divergent series (any series that would add up to infinity) makes a traditional sum meaningless. However, using some mathematical contortion, we can define a new term called the Ramanujan sum. There are other far more complicated ways to demonstrate this, and surprisingly, there are some real world applications to this result. This math trick also has a moral application: nothing in this world is as simple as it seems.